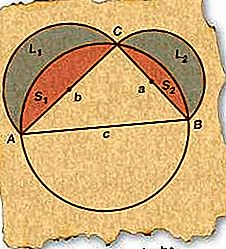
Hipokrāts no Hiosas (fl. C. 460 bc) parādīja, ka mēness formas apgabali starp apļveida arkām, kas pazīstami kā lunas, varētu tikt izteikti precīzi kā taisns laukums vai kvadrāts. Šajā vienkāršajā gadījumā divām plaušām, kas izveidotas ap labā trīsstūra sāniem, kopējais laukums ir vienāds ar trīsstūra laukumu.
-
Sākot ar labo ΔABC, uzvelciet apli, kura diametrs sakrīt ar AB (c puse) - hipotenūzi. Tā kā jebkurš taisnstūris, kas novilkts ar apli ar diametru tā hipotenūzei, ir jāiekļauj aplī, C jābūt uz apļa.
-
Zīmējiet puslokus ar diametru AC (b puse) un BC (puse a) kā parādīts attēlā.
-
Marķējiet iegūtās plaušas L 1 un L 2 un iegūtos segmentus S 1 un S 2, kā parādīts attēlā.
-
Tagad plaušu (L 1 un L 2) summai jābūt vienādai ar to pusloku (L 1 + S 1 un L 2 + S 2) summu, kas satur tos, atskaitot abus segmentus (S 1 un S 2). Tādējādi L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (jo apļa laukums ir π reizes lielāks par rādiusa kvadrātu).
-
Segmentu (S 1 un S 2) summa ir vienāda ar pusloka laukumu, pamatojoties uz AB, no kura atņem trīsstūra laukumu. Tādējādi S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Aizstājot izteiksmi 5. solī 4. solī un faktorējot vispārīgos terminus, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Tā kā ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, izmantojot Pitagora teorēmu. Tādējādi L 1 + L 2 = ΔABC.
Hipokrātam izdevās kvadrātveidīgi izkārtot dažāda veida plaušas, dažas no tām arkas, kas ir lielākas un mazākas par puslokiem, un viņš uzrunāja, kaut arī viņš varbūt neticēja, ka ar viņa metodi var apzīmēt veselu apli. Klasiskā laikmeta beigās Boethius (c. Ad. 470–524), kura Eiklida fragmentu tulkojumi latīņu valodā saglabātu mirgojošu ģeometrijas gaismu pusgadu tūkstošgades garumā, minēja, ka kāds ir paveicis apļa kvadrātu. Nav zināms, vai nezināmais ģēnijs izmantoja plaušas vai kādu citu metodi, jo vietas trūkuma dēļ Boethius nesniedza demonstrāciju. Tādējādi viņš pārsūtīja apļa kvadratura izaicinājumu kopā ar ģeometrijas fragmentiem, kas acīmredzami bija noderīgi tā izpildē. Eiropieši netika galā ar neveiksmīgo uzdevumu apgaismības laikā. Visbeidzot, 1775. gadā Parīzes Zinātņu akadēmija, kurai bija apnicis uzdevums atklāt daudzos tai iesniegtos risinājumos kļūdainus lēmumus, atteicās no tā, ka tam būtu kaut kas vairāk saistīts ar apļa kvadrātiem.




![Vanaga filma Lielais miegs [1946] Vanaga filma Lielais miegs [1946]](https://images.thetopknowledge.com/img/entertainment-pop-culture/6/big-sleep-film-hawks-1946.jpg)