Diferenciālvienādojums

Diferenciālvienādojums, matemātisks paziņojums, kas satur vienu vai vairākus atvasinājumus, tas ir, terminus, kas attēlo nepārtraukti mainīgo lielumu izmaiņu ātrumu. Diferenciālvienādojumi ir ļoti izplatīti zinātnē un inženierzinātnēs, kā arī daudzās citās kvantitatīvo pētījumu jomās, jo tas, ko tieši var novērot un izmērīt sistēmām, kurās notiek izmaiņas, ir to izmaiņu ātrums. Diferenciālvienādojuma risinājums parasti ir vienādojums, kas izsaka viena mainīgā funkcionālo atkarību no viena vai vairākiem citiem; tas parasti satur nemainīgus terminus, kas nav sākotnējā diferenciālvienādojumā. Vēl viens veids, kā to pateikt, ir tāds, ka diferenciālvienādojuma risinājums rada funkciju, kuru var izmantot, lai paredzētu sākotnējās sistēmas uzvedību vismaz noteiktos ierobežojumos.

analīze: Ņūtons un diferenciālvienādojumi

analīzes piemērošana ir diferenciālvienādojumi, kas dažādu lielumu izmaiņu ātrumu saista ar to pašreizējām vērtībām,

Diferenciālvienādojumus klasificē vairākās plašās kategorijās, un tos savukārt iedala vairākās apakškategorijās. Vissvarīgākās kategorijas ir parastie diferenciālvienādojumi un daļējie diferenciālvienādojumi. Ja vienādojumā iesaistītā funkcija ir atkarīga tikai no viena mainīgā, tā atvasinājumi ir parastie atvasinājumi, un diferenciālvienādojums tiek klasificēts kā parasts diferenciālvienādojums. No otras puses, ja funkcija ir atkarīga no vairākiem neatkarīgiem mainīgajiem, tā atvasinājumi ir daļēji atvasinājumi, diferenciālvienādojums tiek klasificēts kā daļējs diferenciālvienādojums. Šie ir parasto diferenciālvienādojumu piemēri:

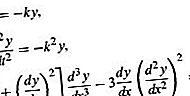
Tajos y apzīmē funkciju, un t vai x ir neatkarīgais mainīgais. Simboli k un m šeit tiek izmantoti, lai apzīmētu īpašas konstantes.

Neatkarīgi no veida, diferenciālvienādojums tiek uzskatīts par n-to pakāpi, ja tas attiecas uz n-tās kārtas atvasinājumu, bet nav atvasinājums no kārtas, kas ir augstāks par šo. Vienādojums ir otrās kārtas daļēja diferenciālvienādojuma piemērs. Parasto un daļējo diferenciālvienādojumu teorijas ir ievērojami atšķirīgas, un šī iemesla dēļ abas kategorijas tiek apskatītas atsevišķi.

Viena diferenciālvienādojuma vietā pētījuma objekts var būt vienlaicīga šādu vienādojumu sistēma. Dinamikas likumu formulēšana bieži noved pie šādām sistēmām. Daudzos gadījumos n-tās kārtas vienādojuma diferenciālvienādojumu ir izdevīgi aizstāt ar n vienlaicīgu vienādojumu sistēmu, no kurām katra ir pirmās kārtas vienādojums, lai varētu pielietot metodes no lineārās algebras.

Parasts diferenciālvienādojums, kurā, piemēram, funkcija un neatkarīgais mainīgais tiek apzīmēts ar y un x, faktiski ir netiešs y būtisko raksturlielumu kopsavilkums kā x funkcija. Domājams, ka šie raksturlielumi būtu pieejamāki analīzei, ja varētu izveidot skaidru formulu y. Šādu formulu vai vismaz vienādojumu x un y (kurā nav atvasinājumu), kas ir secināms no diferenciālvienādojuma, sauc par diferenciālvienādojuma risinājumu. Procesu, kurā no vienādojuma tiek atdalīts vienādojums, izmantojot algebru un aprēķinus, sauc par vienādojuma atrisināšanu vai integrēšanu. Tomēr jāatzīmē, ka diferenciālvienādojumi, kurus var tieši atrisināt, veido tikai nelielu mazākumu. Tādējādi lielākā daļa funkciju jāizpēta ar netiešām metodēm. Pat tā esamība jāpierāda, ja nav iespējas to ražot pārbaudei. Praksē izmanto skaitliskās analīzes metodes, kurās iesaistīti datori, lai iegūtu noderīgus aptuvenus risinājumus.